by Band on the Run 101 Replies latest jw friends
Hint - Do you feel that math is not 'beyond' most folks' comprehension?
Absolutely it is beyond their comprehension.
They should just turn on the TV, log into Facebook, respond to their twitters and forget about it.
- Lime
PS: Oh, and join a religion and/or do drugs. Well, same thing, really, I repeat myself.
@ talesin: I have loved mathematics since I discovered its beauty as a six-year-old boy in the first grade. But I didn't begin to really understand its power and scope until I studied Euclidean geometry in high school and learned the classical axiomatic method. I'm currently writing a science-fantasy novel, Magic Squared, that has mathematics as one of its themes.
@ Nika Bee: I have a special affection for linear algebra. Matrices have always fascinated me and I was fortunate enough to conduct some original research in the field while I was an undergraduate at the University of Colorado. My professors begged me to publish my findings, but I never made the time to write a formal paper. That research is a component of Magic Squared. I am also very fond of the mathematics involved with celestial mechanics. Calculating orbits and spacecraft flight paths has fascinated me since I was twelve years old.
Quendi
BOTR,
I find math fascinating though i only have an understanding of the basic fundamentals. One simple math concept that is inherent in nature and thus physics is the inverse square law which as applied to variables such as distance and intensity is true of many forces and/or effects in the universe. Sound, light, gravity, magnetism, etc all follow this simple rule, which states that as you increase the distance from a source, the intensity or force in question decreases by the inverse square of the distance.
y=1/x 2
If you stand twice as far away from speaker, it will appear 1/4 as loud. If you quad the distance, it is 1/16th as loud. (Note here that we don't hear sound levels in a linear fashion; it's logarithmic but that's another story) Same rule goes for light and brightness, gravity and attraction, etc. A very simple equation that is inherent in much of physics, though much other stuff can be built around it, essentially.
Were you to graph only the positive real numbers;
Ok, pretty but this is the basics of analytic geometry. Nothing much funky about the function but the idea of the cartesian coordinate system is fundamental to many types of math. It has roots in the early Greek geometers and the ideas of Euclid and his planes. But in itself, it's a little tough to make the connection to the concept it describes. Sure one might see that the function doesn't quite cross either axis and deduce that for any real number x, y will never be 0 or infinity. So, it has limits but that is another story. Still not seeing it.
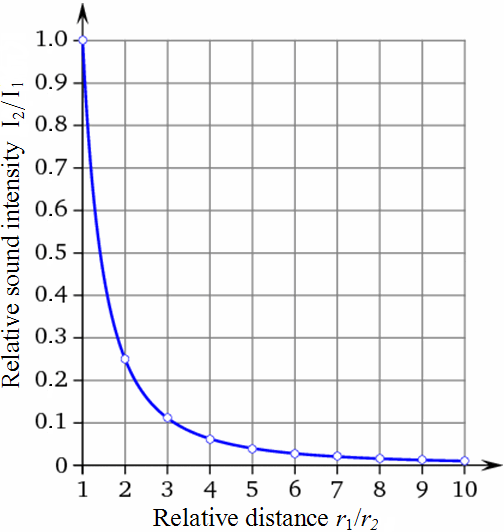
It didn't really click with me until I saw this
Now that's a lot easier to understand and is worth a thousand words IMO. Of course, the effect that's being described is easily seen here though it's still a cartesian system, just with a third axis, z.
If I'm not mistaken, an equation is "derived" from the basic function in the xy coordinate system to this xyz one using calculus and differentiation. It works the other way as well using integration. I stand to be corrected by the professionals here on this though.
So maybe this is kinda something like what you're looking for. Maybe you know it already. But it was fun to try and explain. Kinda weird, eh? ;)
Thanks QUENDI. Apparently I wasn't the only one having problems with the homework assignment - no one in the class got it right! It was all straightened out by the end of class, though. Crazy stuff, but useful.
Try these:
I think this is the future of education. He explains both the math methods, concepts, and examples.
Lots of college lectures.
Tons of educational stuff.
Checkbooks, accounting, finance terms, reading management reports, understanding "math" in contracts (like a mortgage interest amortization schedule) . . . that is what needs to be emphasized to 90% of our population. Unfortunately, our education is focused on classical math.
Maybe so, but 90% of our scientific progress comes about due an understanding of the other type of math. It seems we have far too many Wall Street people and big bankers and tax lawyers and the like who can make money off of basic understandings of things like accounting principles, economic concepts and things like these. We really need more people, especially in America, interested in science and engineering.
The real problem with math is that everyone basically takes up to Calculus which means everyone gets these courses in basic skills, like algebra and trig and differentiation and integration and they stop, just as math is about to get really practical. The algebra and trig that so many high school (and even college) students get so hung up on is almost practically useless by itself. Its only when you get to differential equations and vector calculus and linear algebra and proabability theory that everything starts coming together to solve real world problems and model real world situations.
I wanted to share this with everyone. This video, more than anything else I can say, explains why I am a mathematician. I think that james_woods will especially appreciate it.
http://www.youtube.com/watch?v=kkGeOWYOFoA&list=PL3884F810193DCE51&index=3&feature=plpp_video
Quendi
@ simon17: My mathematics professors at CU would have disagreed with your thesis that real math starts with vector calculus and differential equations. As my all-time favorite teacher told us on the first day of our Advanced Mathematics class: "The preliminaries are over. Differential, integral, vector calculus and differential equations were the preliminaries. Now, your study of real mathematics begins!" As far as he and and the faculties of both the Mathematics and Applied Mathematics Departments at the University of Colorado were concerned, those branches of mathematics weren't even on the radar screen.
I remember being out in field service with a Witness woman who asked me if calculus was the most "advanced" form of mathematics a person could study. When I told her no, she then asked what could possibly be more complicated than calculus. "Arithmetic and algebra are," I answered. She thought I was kidding her, and she replied she had studied both in primary and secondary school. "No," I told her. "You only learned how to use arithmetic and algebra. You did not learn how they really work. I assure you, real arithmetic and real algebra lie on the other side of calculus."
But I get the thrust of your argument and I agree with it. Higher mathematics is not about numbers. It is about thinking both analytically and synthetically and that comes with studying the various disciplines that are beyond calculus.
Quendi
Well yeah, from a mathematician's point of view, just simple ODEs and PDEs have been studied ad nauseam for so long now, that you have to go way higher to get on the cutting edge of REAL mathematics. But I was speaking of people that go into a field that requires math, and those people are usually not going to be applied/pure mathematicians, but rather ChemE, EE, ME, Civil, BioStats, etc and for those people those courses are going to be the foundations of what they need to practically do in their fields.
Also not sure I agree arithmatic and algebra are on the other side of calculus! Calculus is still more advanced than those, even though we dont fully understand them when you do them in high school. After all, once you understand metric spaces and all that, then you're really ready to re-do your calculus and have some fun with Riemann Stieljes Integals and the like.
