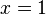0.99999999999 = 1

by nicolaou 24 Replies latest watchtower beliefs

• 

  nicolaou

  
• 

  nicolaou

  Show this to a dub and get them engaged on a discussion of infinity/eternity . . . .
• 

  dazed but not confused

  So many 9's

  
• 

  notsurewheretogo

  A proof that has been put forward for 1 = 0.999, as follows:

  

  

  

  

  

  In the 4th line of the proof we see that from the RHS: 9.999...-0.999... = 9. This is not the case. While it is true that the number of 9s after the decimal point is infinite, it is neither sufficient or trivial to assume this step. For example:

  Take an infinitely long integer consisting exclusively of 9s, call this number A. Take second infinitely long integer also consisting exclusively of 9s and call this number B.

  A - B = 0

  If and only if the number of digits in A and B are the same. Since x has been multiplied by 10, its infinite number of 9s after the decimal point is one less than in x by definition. (sorry to jump in here...but how is one set of INFINITE 9's smaller than another set of INFINITE 9's...by definition, they are the same) It is not sufficient either to say that there are an infinite number of 9s after the decimal place therefore it does not matter, irrespective of whether the repetition is finite or not, the number of digits does need to be the same, and as Mathematicians know, not all infinities are the same. (I laughed. What a joke. Go read some Cantor theorems. infinity +1 is ALWAYS equal to infinity). Therefore the 4th line should say:

  That is only true for a finite series.
• 

  Ding

  Could you please shorten the title of the thread?

  It's so long that it's messing up my screen.

  Thanks.
• 

  Witness My Fury

  Depends on the decimal place...
• 

  bohm

  I remember first seing the proof in school and finding it upsetting - to really resolve the "paradox" one need to consider how the reals are constructed (yes, you build the reals). But its a nice proof to rattle ones high-school intuition
• 

  dazed but not confused
• 

  TheClarinetist

  My personal favorite proof:

  1/3 = 0.3333333

  3 * (1/3) = 1

  0.333333 * 3 = 0.9999999

  therefore 0.999999 = 1.

  Wikipedia has some more proofs (including construction of real numbers), the majority of which are significantly more complicated than my math education allows. What I find interesting is that is works in non-integer bases as well (though with different numbers, of course)
• 

  nicolaou

  (happy to have shortened the Topic title)

  Imagine an infinitely long queue of men and women. If all the women leave, has the queue gotten any shorter?

  Nope. Fun isn't it?